Implementation of MoRE
Contents
System requirements
The following system requirements must be fulfilled to work with MoRE Developer:
- Hardware:
- processor: Intel Xeon or Core i5 or higher or an equivalent AMD processor
- working memory: 8 GB or more
- free hard disk space: 100 GB or more
- screen resolution: at least 1280 * 800 pixel
- Software:
- Windows operating system with.NET-Framework 4.7.2 or higher
For working with MoRE Visualizer, a broadband internet connection is required.
Model architecture and technical implementation of MoRE
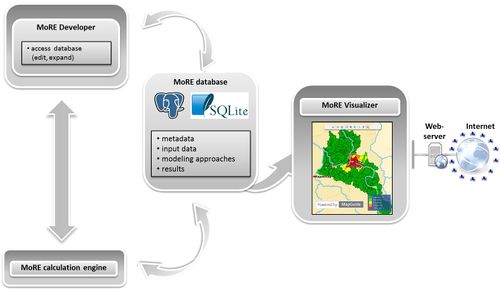
The MoRE system is based on a PostgreSQL/SQLite database, a generic calculation engine and two graphical user interfaces (GUI): the MoRE Developer and the MoRE Visualizer. The GUIs have been developed for user interaction with the database. The database content can easily be read, edited and extended via the MoRE Developer GUI. Modeling is done via a calculation engine which is incorporated in the Developer GUI with a dynamic linkage to the database. Modeling results can be exported as a spreadsheet from MoRE Developer and visualized as a map or chart via a GIS-browser (MoRE Visualizer). MoRE can either be operated by multi user access using a network connection (as an open source PostgreSQL database) or as a single user application for PC (SQLite database).
The MoRE calculation engine
The calculation engine is an independent unit of the MoRE system and programmed in C# as a generic tool, i.e. it only includes the logic structure of the database. It does not include any formulas for the calculation in an executable file. The formulas are stored as plain text in the database. During the model run, the calculation engine reads the input data from the database and calculates according to the defined algorithms of the database. Since the calculation engine is independent from the database, it does not have to be adapted to changes in the modeling approaches, as long as the structure of the MoRE database will be maintained. Thus, the users can run MoRE without having any programming skills. This means that alternative input data, modeling approaches or even another spatial basis for modeling can easily be integrated and tested in MoRE. This makes MoRE a flexible user-friendly modeling tool.
The MoRE database
The MoRE database contains the general and substance specific input data (e.g. analytical units, inhabitants, land use data, water balance, concentration data, etc.) and associated metadata. This means, for example, that each record is assigned a unique origin as well as additional information like pathway specification and substance relation. The database is partitioned into so-called object tables which can be accessed via the MoRE developer’s user interface. It also contains the spatial reference for modeling in terms of analytical units, point sources and planning units. Furthermore, the modeling approaches (empirical equations) are defined in the database. After modeling, the results can be written to and stored in the database or exported for further analysis to MS Excel. The created results can be saved on two levels; as temporary results and as final results. For the visualization, only the final results are used.
The MoRE graphical user interfaces
MoRE Developer
Using the MoRE Developer, new input data can be added to the database and assigned to metadata. Also, modeling approaches can be created and adjusted. Their corresponding informative flow charts can be filed. Additionally, users can access a powerful calculation engine for calculating emissions and river loads for selected analytical units. MoRE is structured in a modular way, so that the approaches of individual pathways can be independently adjusted. Thus, alternative input data sets and modeling approaches can be implemented as variants of a basic variant. This offers the possibility to calculate an emission pathway using different input data sets or different variants of modeling approaches. The results can be compared to evaluate the quality of the considered input data and approaches.
MoRE Visualizer
In addition to the MoRE Developer GUI, the MoRE Visualizer offers the opportunity of presenting and analyzing primary data set and area-specific results. The Visualizer is a GIS browser based application with a direct connection to the MoRE database. All certified changes applied in the MoRE Developer GUI will have a direct effect on results depicted in the MoRE Visualizer. The main use of the Visualizer is to map the area-specific emissions on the level of analytical units from the MoRE database. The data can be selected by different options regarding administrative borders, catchment areas, substances, years and further more. A special feature is the selective comparison of different periods. After the selection and visualization of the data, it can also be presented as reports which can be exported as a spreadsheet file. The MoRE Visualizer automatically summarizes results and shows additional metadata for the selected pathway, substances and aggregation levels. Further options are functions for direct printing and a user-defined classification of displayed values.
Advantages of the MoRE system
The main advantage of MoRE is the way it is implemented: No programming skills are required for working with MoRE. The user can easily import new input data (for instance, new watersheds) or new calculation approaches and test their effects on the modeling results. This is possible due to the generic calculation engine used, which reads the defined input data (and their variants) from the PostgreSQL data base during the calculation run and executes the calculations according to the fundamental modeling approaches (empirical algorithms). Instead of formulas, the calculation engine contains only the logical structure of the data base. Therefore, the engine does not have to be adapted to new algorithms as long as the structure remains the same. Currently, MoRE is used to model water balance, emissions of substances, river loads and costs. It is thereby possible to calculate the respective component separately for each individual analytical unit or to aggregate it along its runoff routing. The substances to be modeled range from nutrients and heavy metals, PAH to e.g. DEHP. Further substances may be added without much effort, provided that a reliable data basis is available. Not least because of its high performance, MoRE is well suited to store and manage the large amount of necessary data. The data can be displayed in tables as well as in form of maps.